2. Transformers e atenção
A arquitetura de transformer 1 revolucionou o campo de processamento de linguagem natural (PLN) e de aprendizado profundo e, atualmente, é o estado-da-arte em tarefas de linguagem. Essa arquitetura é baseada no conceito de atenção, que permite ao modelo descobrir relações entre as diversas partes de um determinado texto.
Arquitetura
A arquitetura de transformer pode variar dependendo da tarefa a ser desempenhada. Nessas anotações, vamos escolher focar na arquitetura que serve de base para os modelos GPT 2 3. Nesse tipo de modelo, o objetivo central é prever qual seria o próximo token mais provável dada uma sequência de tokens, característica de modelos autoregressivos.
Definição (Tokenização 4). A tokenização é o processo de transformar um texto em uma representação semântica compreendido como uma sequência de tokens. Os tokens podem ser palavras, fragmentos de palavras, pontuações ou outros grupos de caracteres. O conjunto de todos os tokens $\mathcal{X}$ de um modelo é chamado de vocabulário.
Observações:
- Em tarefas de linguagem natural, utilizar caracteres individuais como tokens não costuma ser uma boa opção, pois perdemos a propriedade de representar textos semanticamente. Isto é, gostaríamos que algumas sequências de caracteres sejam mais relevantes que outras de acordo com seu uso na linguagem. A sequência “laranja” deveria ser mais importante que “skjsyet”, por exemplo.
- No entanto, utilizar apenas palavras conhecidas do dicionário pode trazer, além de uma quantidade absurda de tokens, dificuldades no processamento de entradas arbitrárias. Por isso, algoritmos como o byte pair encoding (BPE) 5 são utilizados para tornar o processo de tokenização ao mesmo tempo robusto e eficiente.
- Para cada modelo, é comum definir o tamanho do vocabulário como $d_{\text{vocab}} := |\mathcal{X}|$ (dimensão do vocabulário).
O algoritmo de byte-pair encoding é a técnica de tokenização utilizada pelo modelo GPT-2. O processo do algoritmo compreende em realizar agrupamentos de tokens dois a dois até atingir um critério de parada
Podemos, por exemplo, partir de um conjunto inicial de tokens composto pelos caracteres do texto “banana”:
b, a, n, a, n, a.
Para cada iteração do algoritmo, contamos a frequência de todos os pares de tokens adjacentes do texto, e substituímos o par mais frequente por um novo token composto pela concatenação deles. No nosso caso, teríamos um texto tokenizado como b a na na.
Repetimos o passo anterior até atingir o critério de parada (um critério plausível é atingir determinado número de tokens no vocabulário).
Definição (Modelos autoregressivos 4). Seja $\mathcal{X}$ um conjunto de tokens e $\mathcal{X}^N$ um espaço de sequências de tokens de tamanho $N$. Um modelo autogressivo $p : \mathcal{X}^N \to [0, 1]$ induz uma distribuição de probabilidade sobre $\mathcal{X}^N$ atribuindo probabilidade a toda sequência $\mathbf{x} = (x_1, ..., x_N) \in \mathcal{X}^N$ tal que $p(x_1, ..., x_N) = p(x_1) \prod_{n = 2}^N p(x_n | x_1, ..., x_{n-1})$ .
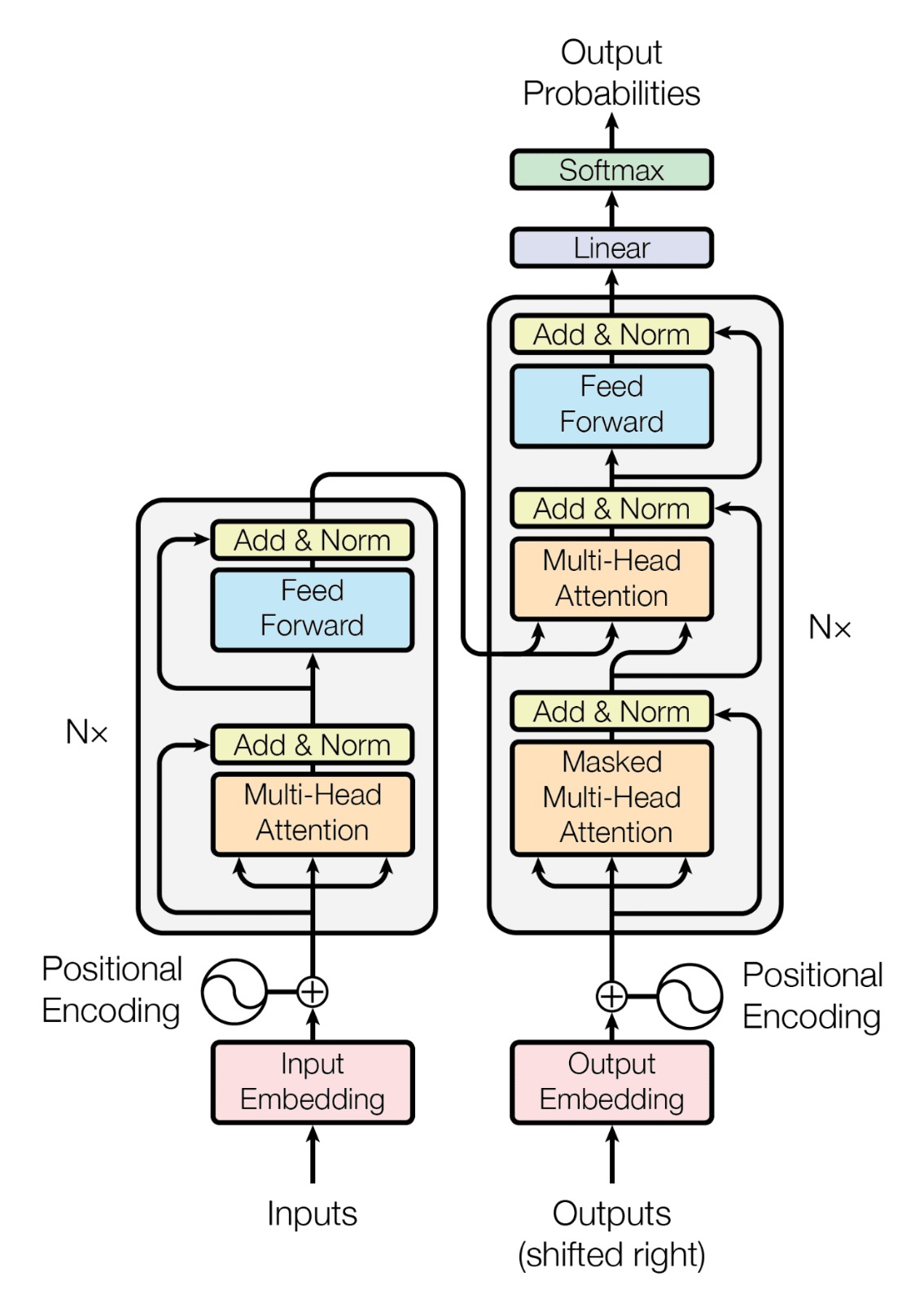
Definição (Transformer 1). A arquitetura original de transformer possui uma estrutura encoder-decoder. O encoder mapeia uma sequência de tokens $\mathbf{x} = (x_1, ..., x_n)$ em uma sequência de representações contínuas $\mathbf{z} = (z_1, ..., z_n)$, vetores de alta dimensão que capturam informações semânticas e contextuais dos tokens de entrada em um espaço contínuo, que chamamos de embedding. A sequência $\mathbf{z}$ posteriormente é utilizada pelo decoder para gerar uma sequência de tokens de saída $\mathbf{y} = (y_1, ..., y_m)$ em conjunto a um novo input, geralmente em tarefas seq2seq. Essas operações são realizadas utilizando o mecanismo de atenção.
Observações:
- Tarefas Seq2Seq são aquelas em que realizamos traduções de um contexto para outro, e dependemos da estrutura completa encoder-decoder. Exemplos de tarefas Seq2Seq são a tradução de texto de uma linguagem para outra e resumo de textos, em que inserimos uma entrada no modelo e esperamos como saída uma versão resumida.
Figura 1. Representação gráfica da arquitetura de transformer do artigo original 1
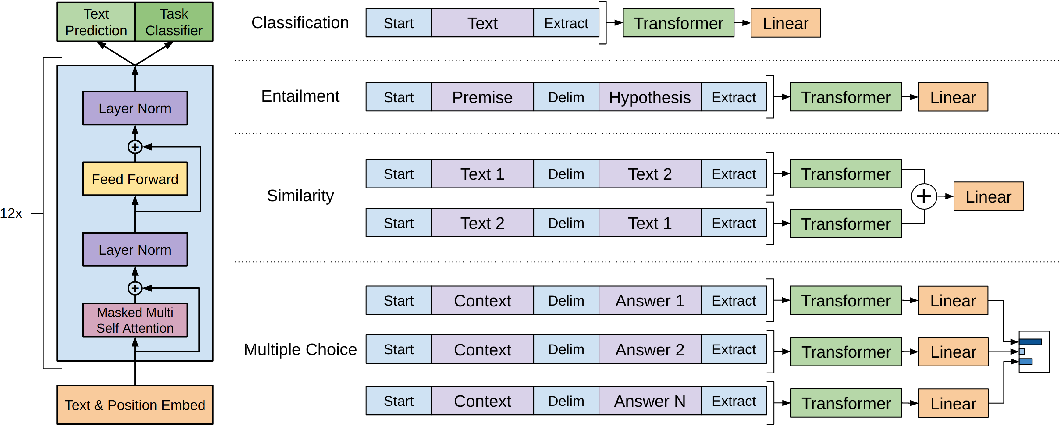
Figura 2. Representação gráfica da arquitetura baseada em transformer do GPT-1 2
Observações:
- Uma intuição inicial do modelo encoder-decoder é a ideia de utilizar um encoder para capturar o contexto entre sequências de tokens de entrada utilizando atenção, produzindo hidden states (representações intermediárias). Mais tarde, o decoder é usado para gerar sequências de tokens com base no último hidden state produzido pelo encoder, e recursivamente adicionando o output token produzido pelo decoder a cada time step.
- A figura 1 ilustra a definição de transformer, mostrando os blocos de encoder e decoder da arquitetura de transformer. No entanto, o GPT (ilustrado na figura 2) se baseia em uma arquitetura que utiliza apenas o decoder da arquitetura original. Isto porque o GPT mapeia os tokens de uma sentença em um vetor de probabilidade para cada token do vocabulário.
- Nem todos os transformers são encoder-decoder, já que essa arquitetura foi desenvolvida para situações em que desejamos mudar de um contexto para outro (isto é, temos uma tarefa Seq2Seq), como traduções. Para tarefas de classificação, por exemplo, utilizar apenas um encoder, enquanto em tarefas de geração de texto no mesmo contexto, um decoder pode ser suficiente.
Componentes e técnicas
Definição (Embedding). Embedding é a representação vetorial dos tokens de um texto em um espaço latente de alta dimensão $\mathbb{R}^{d_\text{embed}}$, sendo $d_\text{embed}$ a dimensão escolhida para o espaço de embedding.
Observações:
- Modelos como o GPT aprendem uma matriz de pesos $W_E$ (também chamada de tabela de consulta de embeddings), que transforma a versão vetorial one-hot-encoded de um token $x_i \in [0, 1]^{d_\text{vocab}}$ (onde somente a $i$-ésima entrada de $x_i$ é igual a 1) em um vetor de dimensão $1 \times d_\text{embed}$:
- Tabelas de consulta de embeddings são obtidas a partir de modelos pré-treinados de word embedding, como o Word2Vec 6.
- É esperado que o modelo consiga aprender a representar cada característica semântica de um token em uma dimensão do espaço latente, como será discutido na seção de Superposição. No entanto, é possível que o modelo acabe representando um número maior de propriedades do que o número de dimensões do espaço latente, fenômeno conhecido como superposição 7. ]
Definição (Positional Embedding). Positional embedding é um embedding adicional com informações posicionais de cada token adicionado ao embedding do texto.
Observações:
- A proposta do Transformer é reconhecer que as posições não são o único determinante de relevância entre tokens, como ocorre nas convoluções. No entanto, a linguagem natural conta com localidade (adjetivos, por exemplo, tendem a se referir ao substantivo mais próximo na sentença), e essa informação é útil ao modelo.
Definição (Fluxo residual). Componente de modelos de deep learning em que a entrada $\mathbf{x}_{i-1}$ de uma camada intermediária $i$ é somada com sua saída $f_i (\mathbf{x}_{i-1})$, permitindo a preservação de informações anteriores:
$$ \mathbf{x}_{i} = f_i (\mathbf{x}_{i-1}) + \mathbf{x}_{i-1}. $$
Observações:
- Se a função ideal a ser aprendida por essa camada for a função identidade, essa implementação tira a necessidade de $f_i$ aprender como reconstruir totalmente a entrada, já que só seria necessário garantir que, para todo $\mathbf{x}_i$, $f_i (\mathbf{x}_{i-1}) = 0$.
- Essa técnica também ajudar a mitigar problemas de vanishing gradient durante o treinamento, isto é, ao realizarmos sempre a soma de saídas de cada camada, evitamos um problema comum em redes neurais profundas em que gradientes das camadas iniciais se tornam extremamente pequenos durante o backpropagation (conforme os gradientes são propagados para trás por várias camadas, eles podem diminuir exponencialmente, interrompendo o fluxo de informação).
- A arquitetura do Transformer utiliza um fluxo residual, essencial para sua memória e fluxo de informações, mantendo informações das camadas anteriores. Assim, os valores no fluxo representam o acúmulo de todas as inferências feitas até aquele ponto. ]
As keys ($K$), queries ($Q$) e values ($V$) são elementos fundamentais em mecanismos de atenção. Eles são obtidas através de projeções lineares, onde os embeddings dos tokens são multiplicados por matrizes de projeção $W^K$, $W^Q$ e $W^V$ aprendidas durante o treinamento. As keys representam o token de origem, as queries representam os tokens de destino e os values representam a semântica e contexto dos tokens.
$W^K$, $W^Q$ e $W^V$ são matrizes de pesos que são ajustadas durante o treinamento. Cada uma dessas matrizes tem dimensões específicas que dependem da dimensão do embedding de entrada ($d_\text{embed}$) e da dimensão desejada para keys, queries e values ($d_k$, $d_q$, $d_v$).
Façamos uma analogia para o funcionamento de um transformer para clarificarmos o conceito de keys, queries e values. Imagine uma fila de pessoas, em que cada um possui um token, e seu objetivo é descobrir o token da pessoa a sua frente. Cada pessoa pode passar perguntas para quem está atrás de si na fila (jamais para frente), e qualquer um atrás pode escolher responder, passando informação para quem fez a pergunta.
Portanto, para a frase O João entregou um pão para Maria., a primeira pessoa possui o token O, a segunda possui o token João, e assim por diante
- Cada pessoa na fila representa um vetor no fluxo residual. Inicialmente, só possuem informações do seu próprio token, mas conforme perguntam e recebem respostas passam a armazenar mais informações.
- A operação executada por um head de atenção é representada por um par pergunta-resposta:
- A pessoa que pergunta é o token de destino, as pessoas que respondem são os tokens de origem;
- A pergunta é a query;
- A informação que determina quem responde à pergunta é a key;
- A informação que é passada de volta para quem fez a pergunta é o value.
Nesse contexto, um processo razoável seria o seguinte:
- A pessoa com o terceiro token (
entregou) pergunta “Alguém tem um token com um sujeito?”, realizando uma query; - A primeira e a segunda pessoas da fila (únicos tokens anteriores a
entregou) acordam entre si que entre seus dois tokens,Joãoé o único que representa um sujeito, decisão que representa a influência da key; - A pessoa com o token
Joãoinforma o token atual que ele próprio é o sujeito, que portanto está na segunda posição. Essa informação repassada representa o value.
Definição (Atenção 1). Atenção é uma função que mapeia uma query e pares de key-value em uma saída, calculada como a soma ponderada dos valores por uma medida de compatibilidade da query com a key correspondente. A função de atenção mais utilizada em transformers é a atenção do produto escalonado, definida como:
$$ \text{Attention}(Q, K, V) = \text{softmax} \left( \frac {Q K^T} {\sqrt{d_k}} \right) V. $$
Observações:
- O produto $Q K^T$ é escalado pela raiz quadrada de $d_k$ (dimensão dos vetores keys e values) para evitar que o resultado cresça muito para valores altos de $d_k$, o que poderia levar a gradientes muito próximos de 0.
- O objetivo da atenção é realizar o fluxo de informação entre os tokens do input. Isto é, para um token de origem (key) calculamos a atenção para todos os tokens de destino (queries).
- Na arquitetura original do Transformer e em diversas aplicações até hoje, utiliza-se a atenção causal (atenção com masking para tokens futuros), impedindo que informação de tokens futuros influenciem tokens passados. Em outras aplicações, como o BERT 8, utiliza-se atenção bidirecional, que permite o fluxo de informação nos dois sentidos.
- Normalmente, ao invés de realizarmos uma única aplicação da função de atenção, computamos várias atenções em paralelo, concatenando os resultados e projetando o resultado de volta para a dimensão do modelo. Essa técnica é conhecida como multi-head attention e visa capturar diferentes dependências entre os tokens.
Definição (Multi-Layer Perceptron (MLP)). Arquitetura de rede neural que consiste em múltiplas camadas totalmente conectadas de nós com ativações não-lineares. Obtemos o output do nós $k$ através do input $z$, do peso $w_k$ e de uma função de ativação $g$:
$$ z_k = g \left( \sum_j w_{j k} z_j \right) $$
Observações:
- No contexto de transformers, tratamos de rede neural padrão com uma única camada oculta e uma função de ativação não linear. Durante a MLP, não há mais fluxo de informação entre os tokens, e opera-se em cada posição do fluxo residual de forma independente, com os mesmos parâmetros.
- A intuição é que a MLP é responsável por armazenar o conhecimento adquirido pela camada de atenção, liberar espaço no fluxo residual e introduzir não-linearidade, permitindo que o modelo capture padrões complexos nos dados.
Definição (Amostragem). Processo de seleção de um subconjunto representativo de dados de um conjunto de dados maior. No contexto de Machine Learning, tratamos da obtenção dos outputs esperados para a tarefa a partir dos resultados obtidos em modelos.
Observações:
- Em transformers autoregressivos, quando obtemos os logits, podemos amostrar simplesmente utilizando o token com maior probabilidade como predição. Essa forma de amostragem, no entanto, gera outputs repetitivos. Amostrar a partir de uma distribuição de probabilidade dos logits, por outro lado, leva à perda de coerência das frases geradas.
- Assim, utiliza-se técnicas como o Top-K Sampling, em que amostramos a partir das k probabilidades mais altas.
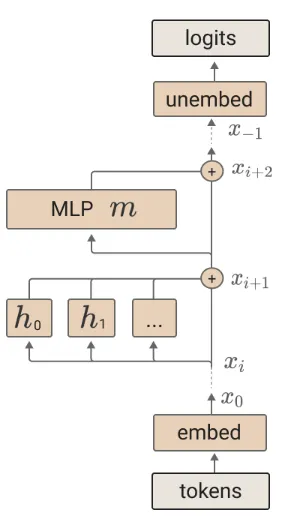
A arquitetura do transformer autoregressivo utilizado tem a seguite abstração de alto nível:
Assim, o processo de treinamento do modelo se dá reunindo os conceitos definidos até então. A partir da tokenização dos inputs e do subsequente embedding dos tokens, temos os inputs em forma de vetores de informação. Em seguida passamos pelos blocos residuais, compostos por:
- Um attention block, em que o resultado de cada attention head adicionado ao fluxo residual:
- Um feed-forward block, isto é, um MLP, em que o resultado também é adicionado ao fluxo residual:
Por fim, realizamos um unembedding, que converte nosso fluxo residual em logits. Um logit é um valor real que representa a propensão relativa de cada token do vocabulário ser o próximo na sequência. Para transformar esses logits em probabilidades, aplicamos a função softmax, que normaliza os logits para que a soma das probabilidades seja 1. Dessa forma, cada probabilidade resultante indica a chance de um token específico ser o próximo na sequência, e escolhemos a forma de amostragem de modo que haja variabilidade.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł. ukasz, & Polosukhin, I. (2017). Attention is All you Need. Advances in Neural Information Processing Systems, 30. https://papers.nips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html ↩︎ ↩︎ ↩︎ ↩︎
Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving language understanding by generative pre-training. https://www.mikecaptain.com/resources/pdf/GPT-1.pdf ↩︎ ↩︎
Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., & Sutskever, I. (2019). Language models are unsupervised multitask learners. OpenAI Blog, 1(8), 9. https://insightcivic.s3.us-east-1.amazonaws.com/language-models.pdf ↩︎
Bishop, C. M., & Bishop, H. (2024). Deep Learning: Foundations and Concepts. Springer International Publishing. https://doi.org/10.1007/978-3-031-45468-4 ↩︎ ↩︎
Sennrich, R., Haddow, B., & Birch, A. (2016). Neural Machine Translation of Rare Words with Subword Units. arXiv. https://doi.org/10.48550/arXiv.1508.07909 ↩︎
Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient Estimation of Word Representations in Vector Space. ↩︎
Elhage, N., Hume, T., Olsson, C., Schiefer, N., Henighan, T., Kravec, S., Hatfield-Dodds, Z., Lasenby, R., Drain, D., Chen, C., Grosse, R., McCandlish, S., Kaplan, J., Amodei, D., Wattenberg, M., & Olah, C. (2022). Toy Models of Superposition. Transformer Circuits Thread. ↩︎
Devlin, J., Chang, M.-W., Lee, K., & Toutanova, K. (2018). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. CoRR, abs/1810.04805. http://arxiv.org/abs/1810.04805 ↩︎