5. Superposição

A superposição acontece quando um modelo representa mais de $n$ features em um espaço de ativações $n$-dimensional. Esse fenômeno pode acontecer dependendo da distribuição dos dados e suas features. Para conseguir estudar e replicar esse fenômeno, o artigo “Toy Models for Superpostion” ¹ propõe modelos simples (chamados de modelos de brinquedo, ou toy models) que servem para testar vários modelos simultaneamente, variando aspectos dos dados e do próprio modelo.

Definição (feature) Uma feature é alguma característica dos dados de entrada que pode ser representada pelo modelo como direções no espaço latente.

Observações:

• O entendimento do que é realmente uma feature pode ser confuso. Uma feature pode ser tanto uma característica simples do dado de entrada (ex.: se uma foto contém um gato ou não) ou algo que não é tão interpretável a primeira vista.

É natural pensar que, dado que o modelo representa features como direções, só seria eficiente para o modelo representar uma quantidade de features no máximo igual ao que ele possui de dimensões. Por exemplo, características de uma imagem como ter um gato ou um carro aparentam ser independentes, sendo mais eficiente dar direções ortogonais para essas duas features. No entanto, a importância ou probabilidade de certa feature pode afetar como o modelo vai representá-la.

Definição (importância de uma feature) A importância $I_i$ de uma feature $i$ é o quão útil esta feature é para atingir uma loss mais baixa.

Definição (probabilidade de uma feature) A probabilidade $p_i$ de uma feature $i$ é a probabilidade dessa feature ser diferente de zero no conjunto de dados.

Observações:

• Podemos interpretar a probabilidade de uma feature como uma medida complementar a uma medida de esparsidade (i.e., $S_i = 1 - p_i$): se uma feature possui uma baixa probabilidade, isso implica que essa feature é muito esparsa. Essa noção será útil ao analisar os gráficos do nosso modelo de brinquedo.
• O modelo de brinquedo a ser utilizado é o ReLU output model, definido como $ h = W x, x' = \text{ReLU}(W^T h + b), $ onde $W \in \mathbb{R}^(2 \times 5)$ é uma matriz de pesos e $b \in \mathbb{R}^2$ é um vetor de bias.
• A loss é dada por $L = \frac 1 {B F} \sum_x \sum_i I_i (x_i - x'_i)^2$, onde $I_i$ é a importância que damos para a feature i, $B$ é o tamanho do batch e $F$ é a quantidade de features.
• A partir da imagem abaixo, é possível observar que existem duas tendências conflituosas no processo de treinamento: 1) representar mais features, que é considerado desejável, e 2) reduzir interferência entre as features, já que também é interessante representar features ortogonalmente.

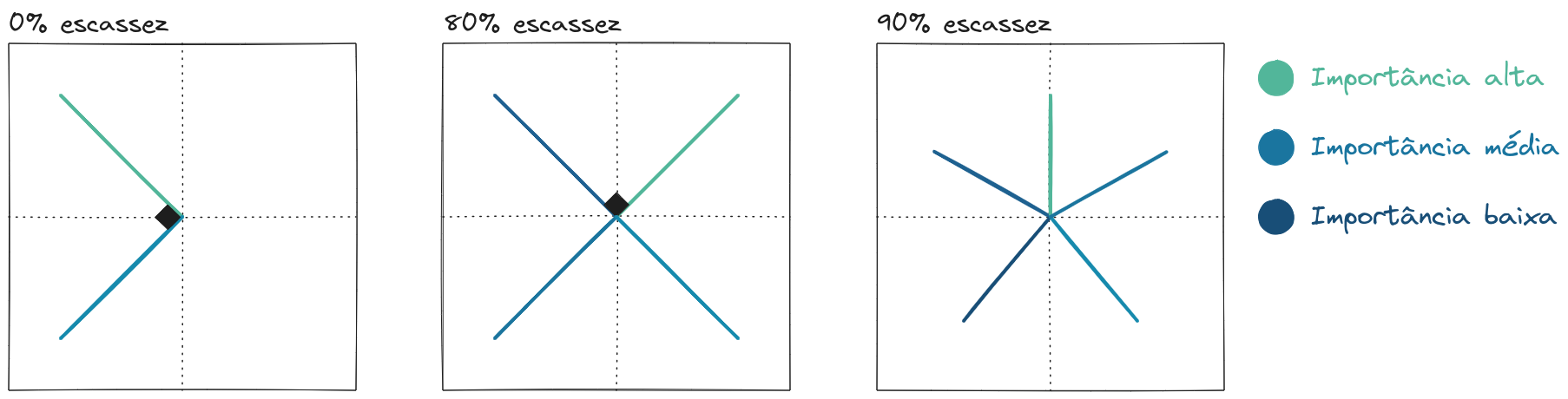
Gráfico dos pesos aprendidos pelo modelo de brinquedo de duas dimensões a depender da escassez das features (que são 5 no total.) Se a esparsidade é baixa, o modelo dedica exclusivamente as duas dimensões para as features mais importantes. Se a esparsidade aumenta, o modelo chega a comportar todas as 5 features em um espaço de duas dimensões, causando um efeito de interferência entre as features.

Outra propriedade das features que afeta como o modelo as representa é a correlação entre elas. Assim como uma baixa probabilidade das features incentiva superposição, esperaríamos que a presença de features anti-correlacionadas também incentive esse fenômeno.

Definição (correlação entre features) Duas features são correlacionadas se elas aparecem juntas em um conjunto de dados. Analogamente, duas features são anti-correlacionadas se a aparição de uma delas está ligada a não aparição da outra.

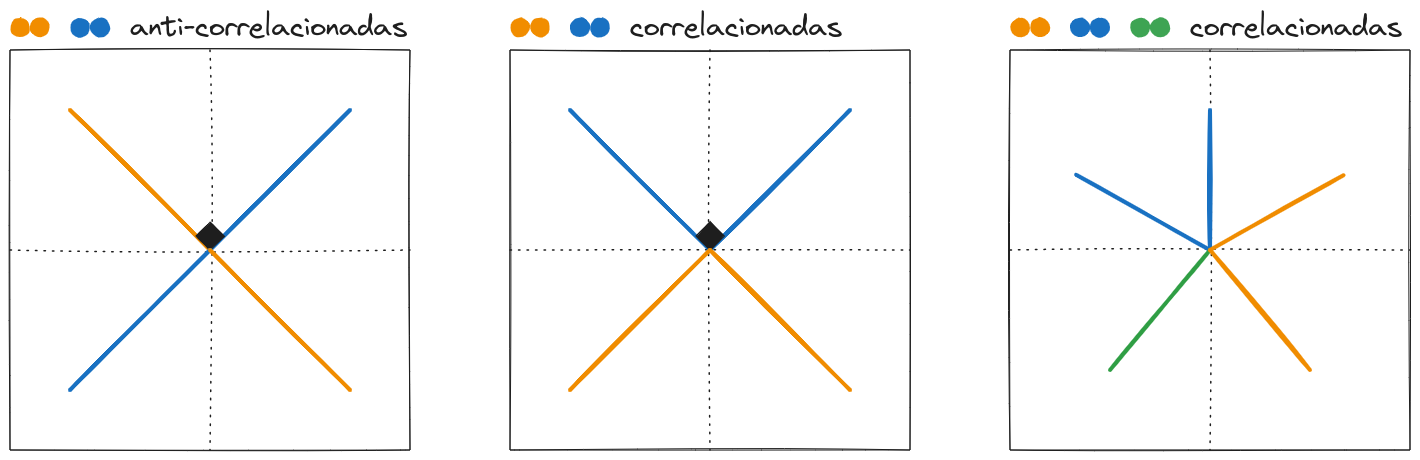
Gráfico dos pesos aprendidos pelo modelo de brinquedo a depender da correlação das features. Modelos tendem a representar features correlacionadas em dimensões ortogonais (ou lado a lado se não for possível representá-las ortogonalmente) e tendem a representar features anti-correlacionadas em direções opostas.

Observações:

• A maioria das features normalmente encontradas são anti-correlacionadas. Por exemplo, raramente um texto será classificado, ao mesmo tempo, como um código Python e como uma ficção científica.

Assim, os fenômenos acima levam à ampla ocorrência de superposição em modelos de aprendizado de máquina. Não é possível estabelecer uma relação direta entre uma feature e um neurônio (ou ativações), e não há uma base interpretável.