3. Mechanistic Intepretability
A proposta da mechanistic interpretability é, a partir de um modelo pré-treinado, utilizar ténicas de engenharia reversa para descobrir algoritmos aprendidos pelo modelo a partir de seus pesos. Esse tipo de investigação é realizada com o objetivo de compreender melhor como o modelo se comporta em certas situações.
Modelos de aprendizado de máquina são descritos como black box, já que não conhecemos seu funcionamento. É importante que os modelos que treinamos tenham explicabilidade em diversos âmbitos. Em certas tarefas, como decisões de crédito, explicar as decisões do modelo a partes interessadas pode ser crucial para confiabilidade. Além disso, a interpretabilidade também desempenha um papel importante na segurança de modelos de inteligência artificial, já que compreender o funcionamento interno do modelo nos leva a aprimorar robustez de possíveis áreas de falha e compreender o impacto de decisões.
Observações:
- Os conteúdos discutidos a partir de agora são frutos de aplicações bem práticas da teoria apresentada, e tem suporte para implementação na biblioteca TransformerLens, desenvolvida por Neel Nanda para mechanistic interpretability em modelos de linguagem similares ao GPT-2. O objetivo da biblioteca é facilitar o acesso e permitir modificações em partes internas do modelo, simplificando o processo de engenharia reversa.
- O foco principal desse handbook é discutir os conceitos teóricos de mechanistic interpretability em transformers, mas encorajamos fortemente a exploração da biblioteca. Para isso, recomendamos o apoio da fonte inpiradora deste conteúdo (capítulo 1 do ARENA 3.0 1).
Circuitos
Quando estudamos redes neurais profundas, nos deparamos quase certamente com grandes redes cheias de neurônios que se ativam sem um padrão muito claro. O estudo de circuitos visa entender a relação das camadas e os pesos com as ativações e descobrir os algoritmos que emergem do treinamento dessas redes neurais.
Definição (ativação). A ativação de um nó em um forward pass é o valor associado a esse nó durante a propagação a partir de uma determinada entrada, i.e., o valor de $f_{\eta}(\mathbf{x})$, onde $f_{\eta}$ é a função que descreve o nó $\eta$ e $\mathbf{x}$ é uma entrada qualquer.
O termo ativação é bastante utilizado pela comunidade de interpretabilidade em múltiplos contextos. Façamos uma desambiguação do termo para tornar a leitura deste handbook mais clara:
Ativação como valor resultante de um forward pass: trata-se de um valor associado à saída de um neurônio e repassado ao próximo, alterado a cada propagação.
Função de ativação: trata-se de uma função aplicada à combinação linear de entradas e pesos obtida pela saída de um neurônio. As funções de ativação introduzem não-linearidade no modelo, permitindo que aprendizado de padrões complexos. Podemos citar como exemplo as funções ReLU e sigmoide.
Ativação de uma head de atenção: processo pelo qual uma head de atenção identifica e foca em partes específicas do input durante o cálculo da atenção. Quando uma head de atenção “se ativa” (ou “dispara”), ela está destacando certas informações no contexto da sequência de entrada, permitindo que o modelo preste atenção a diferentes aspectos do dado em diferentes heads e aprenda.
Observações:
- Por exemplo, scores de atenção (i.e., o produto escalado por $d_k$ entre as queries e as keys) são ativações.
- É importante distinguir ativações de parâmetros (que são os pesos e vieses aprendidos durante o treinamento e não mudam dependendo da entrada.).
Definição (Circuito 2). Um circuito é um sub-grafo de uma rede neural que consiste em um conjunto de propriedades intimamente ligadas com seus pesos.
O entendimento de circuitos em transformers se baseia fortemente no conhecimento das matrizes de pesos que servem de base para seu funcionamento.
Seja um modelo de multi-head attention, ou seja, que realiza várias operações de atenção em paralelo ao mapear embeddings intermediários da dimensão interna do modelo para a dimensão de head. Identificaremos objetos específicos de cada head com um sobrescrito ${(\cdot)}^h$. Seja, também,
- $d_\text{model}$ a dimensão interna do modelo;
- $d_\text{head}$ a dimensão de cada head do modelo, normalmente definido como $d_\text{head} = d_\text{model} / n_\text{head}$, onde $n_\text{head}$ é o número de heads;
- $d_\text{vocab}$ a dimensão do vocabulário;
- $n_\text{ctx}$ o número máximo de tokens que o modelo consegue processar (janela de contexto);
- $W^h_K \in \mathbb{R}^{d_\text{model} \times d_\text{head}}$ a matriz de pesos para as keys;
- $W^h_Q \in \mathbb{R}^{d_\text{model} \times d_\text{head}}$ a matriz de pesos para as queries;
- $W^h_V \in \mathbb{R}^{d_\text{model} \times d_\text{head}}$ a matriz de pesos para os values;
- $W^h_O \in \mathbb{R}^{d_\text{head} \times d_\text{model}}$ a matriz de pesos para a saída;
- $W^h_E \in \mathbb{R}^{d_\text{vocab} \times d_\text{model}}$ a matriz de pesos para embedding;
- $W^h_U \in \mathbb{R}^{d_\text{model} \times d_\text{vocab}}$ a matriz de pesos para unembedding;
- $W_\text{pos} \in \mathbb{R}^{n_\text{ctx} \times d_\text{model}}$ a matriz de pesos para positional embedding.
Temos as seguintes matrizes:
- $W^h_\text{OV} \in \mathbb{R}^{d_\text{model} \times d_\text{model}} = W^h_V W^h_O$, que descreve qual informação se move da fonte até o destino no fluxo residual. Chamaremos de circuito OV.
- $W_E W^h_\text{OV} W_U \in \mathbb{R}^{d_\text{vocab} \times d_\text{vocab}}$, que descreve qual informação se move da fonte até o destino do início ao fim. Chamaremos de circuito OV completo.
- $W^h_\text{QK} \in \mathbb{R}^{d_\text{model} \times d_\text{model}} = W^h_Q W^h_K$, que descreve de onde e para onde as informações se movem no fluxo residual. Chamaremos de circuito QK.
- $W_E W^h_\text{QK} (W_E)^T \in \mathbb{R}^{d_\text{vocab} \times d_\text{vocab}}$, que descreve de onde e para onde as informações se movem entre os tokens do vocabulário. Chamaremos de circuito QK completo.
- $W_\text{pos} W^h_\text{QK} (W_\text{pos})^T \in \mathbb{R}^{n_\text{ctx} \times n_\text{ctx}}$, que descreve de onde e para onde as informações se movem entre os tokens no contexto (i.e., entre as posíções) circuito QK completo de posições.
Observações:
- Imagine que queremos analisar se uma determina head $h$ está dando mais atenção para o token imediatamente anterior a todo token. Conseguiríamos descobrir se isso é verdade ao constatar que o circuito QK completo de posições, $W_\text{pos} W^h_\text{QK} (W_\text{pos})^T$, é uma matriz que possui valores altos nas entradas logo abaixo da diagonal. Ou seja, dá um score alto para o token anterior.
- Outro comportamento bem comum estudado pela ótica de circuitos é o de indução, no qual o modelo atribui um score maior para sequência de tokens que já apareceram no texto. Ou seja, o modelo aprende a identificar aparições anteriores de um mesmo token e a considerar o próximo token da aparição anterior como um bom candidato a ser o próximo do atual token.
Heads e circuitos de indução
Definição (Attention patterns). Comportamentos que observamos em heads de atenção que descrevem o tipo de relação entre tokens capturadas por um head. Destacam-se os seguintes padrões:
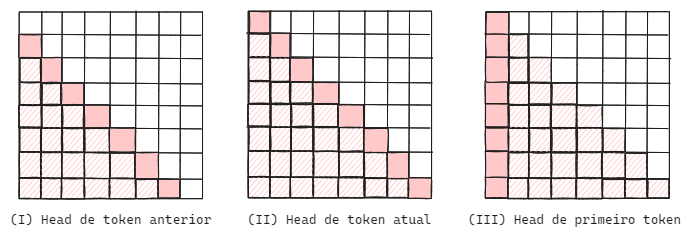
- Head de token anterior: voltam a atenção ao token anterior na sequência;
- Head de token atual: voltam a atenção ao próprio token na sequência;
- Head de primeiro token: voltam a atenção ao primeiro token da sequência, em geral uma flag de
<|endoftext|>.
Observações:
- Em interpretabilidade, temos interesse em detectar esse tipo de comportamento, e compreender que tipo de informação cada head captura.
- Os dois primeiros padrões podem parecer mais razoáveis. A intuição para as heads de primeiro token é que a primeira posição funciona como uma posição nula para heads que não ativam com frequência.
Suponha que estamos computando a atenção em uma sequência:
<|endoftext|> Eu amo viajar para lugares legais .
Temos interesse em visualizar a atenção computada por cada head, e produzimos gráficos como os seguintes:
Cada gráfico representa um possível tipo de padrão de atenção. Para uma head qualquer, poderíamos observar que o padrão obtido é de head de token anterior (I), head de token atual (II), head de primeiro token (III), ou mesmo não observar nenhum padrão, havendo uma distribuição de atenção de outras formas.
Note que a biblioteca TransformerLens facilita a exploração e visualização dos padrões, e também sua detecção. Detectar automaticamente o padrão de attention heads nos ajuda a quantificar nossas observações sobre processos internos do modelo.
Definição (Heads de indução). Heads de indução são heads de atenção que realizam um padrão específico, procurando na janela de contexto por exemplos do token atual. Quando o encontram, replicam o próximo token do contexto.
Observações:
- Na prática, heads desse tipo fazem induções da forma
[a][b] … [a] → [b]. - Não é possível ter heads de indução em modelos de uma camada.
- Em modelos com heads de indução, dada uma sequência repetida de tokens, o modelo consegue prever a segunda parte da sequência. A Figura 1 mostra a melhora da habilidade de predição no momento em que a sequência de tokens começa a se repetir:
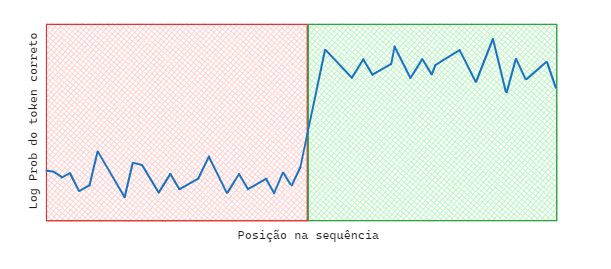
Figura 1. Gráfico da log-probabilidade do token correto por posição em uma sequência com repetição completa de tokens
Observações:
- A observação de heads de indução passa a ocorrer conforme aumentamos a escala do modelo. Para 2 bilhões de tokens há ausência de heads de indução e em 4 bilhões observamos essa capacidade muito bem desenvolvida. Chamamos desenvolvimentos repentinos como esse de capacidade emergente 3.
- Capacidades emergentes são bastante interessantes, mas trazem preocupações no ramo de alinhamento de IA, já que são características que não podem ser previstas treinando modelos de pequena escala. O assunto é pauta de muitos estudos, já que existe discordância se a observação dessas características é fruto da utilização de métricas descontínuas 4.
Definição (Circuito de indução). Um circuito de indução é (normalmente) composto pela composição das seguintes heads:
- Uma head de token anterior, chamado de circuito QK de token anterior.
- Uma head de indução que possui os dois seguintes mecanismos: 1. Atribui um score alto para quando um token $x_i$ é o mesmo token $x_j$ identificado pela head de token anterior, chamado de K-composição. 2. Copia o token que vem logo depois de $x_i$ (i.e., atribui um score alto para o token de $x_{i+1}$ na posição $j+1$ quando $x_i = x_j$), chamado de circuito OV de cópia.
Observações:
- É importante que, nesse ponto, a diferença entre heads de indução e circuitos de indução esteja clara, já que trataremos de diversos circuitos. Um circuito de indução é um circuito composto por um head de token anterior em uma camada passada (responsável por gerar atenção entre a cópia do token atual e seu token seguinte) e uma head de indução. Isto é, circuitos são conjuntos de heads capazes de realizar uma tarefa.
Para compreendermos melhor o funcionamento geral do modelo, é importante compreender o impacto de cada componente. Isto é, quanto da performance do modelo em certa tarefa deve ser atribuído a cada componente?
No contexto de transformers, temos interesse em saber o impacto de cada head no resultado. Para isso, construímos ferramentas que auxiliam no processo, por exemplo:
- Atribuição de logits: os outputs finais de um modelo são logits provenientes do fluxo residual, que são a soma da contribuição de cada camada. Podemos, portanto, decompor esses logits em valores vindos de cada head e compreender melhor o impacto de diferentes heads no resultado.
- Ablation: investigação do desempenho do modelo removendo componentes para entender sua contribuição. No contexto de transformers, podemos suprimir certas heads alterando seus valores para zero e compreender o impacto da mudança no resultado.
Engenharia reversa do circuito de indução
O objetivo de realizar engenharia reversa é entender melhor o funcionamento dos modelos. Queremos saber não apenas que tarefa cada parte de um modelo realiza, mas também o porquê.
Vejamos um exemplo de engenharia reversa para o circuito OV. Sabemos que esse circuito é dado por $W_E W^h_\text{OV} W_U$, mas os únicos fatores interpretáveis do circuito são os tokens de input e os logits de output. Desejamos analisar a própria matriz de pesos.
Como estamos tratando de indução, imagine que temos um input A B … A B. Nesse caso, sendo $b$ o one-hot-encoding de B, $b^T W_E W^h_\text{OV} W_U$ é o vetor de logits movido do primeiro token B para o segundo A, utilizado por este como predição. Assim, esperamos ter uma predição com alta probabilidade de B.
Vamos quebrar em partes para clarificação:
- $b^T W_E$ é o embedding de
B - $b^T W_E W^h_\text{OV}$ é o vetor movido do primeiro token
Bpara o segundoA - $b^T W_E W^h_\text{OV} W_U$ é o vetor de logits representando o impacto da head de atenção $h$ na predição do token após o segundo
A. Representa a cópia deBpara o segundoA.
Como B é copiado para o token atual, $b^T W_E W^h_\text{OV} W_U$ resulta em valores altos na diagonal (o elemento $($B$, X)$ da matriz deve ser mais alto para $X=$B, e portanto temos uma head de token atual).
Observe como a análise detalhada das matrizes de pesos e a engenharia reversa do circuito de indução nos permitem identificar como os modelos de aprendizado profundo utilizam representações internas para realizar previsões. Ao decompor as operações, podemos entender que o embedding de $b$ é transformado e movido pelo circuito e, finalmente, traduzido em logits pela matriz $W_U$.
O entendimento de como o processo se dá é crucial para melhorar a interpretabilidade e a confiança nos modelos, permitindo ajustes mais precisos nas arquiteturas e pesos para melhorar seu desempenho em tarefas específicas.
ARENA Chapter 1: Transformer Interpretability. (n.d.). https://arena3-chapter1-transformer-interp.streamlit.app/ ↩︎
Olah, C., Cammarata, N., Schubert, L., Goh, G., Petrov, M., & Carter, S. (2020). Zoom In: An Introduction to Circuits. Distill. https://doi.org/10.23915/distill.00024.001 ↩︎
Wei, J., Tay, Y., Bommasani, R., Raffel, C., Zoph, B., Borgeaud, S., Yogatama, D., Bosma, M., Zhou, D., Metzler, D., Chi, E. H., Hashimoto, T., Vinyals, O., Liang, P., Dean, J., & Fedus, W. (2022). Emergent Abilities of Large Language Models. ↩︎
Schaeffer, R., Miranda, B., & Koyejo, S. (2023). Are Emergent Abilities of Large Language Models a Mirage? ↩︎